CFD 기초 : 1-D Diffusion problem (1) - 과정설명 / 수식유도
| 본 글 내용은 An Introduction to Computational Fluid Dynamics 2ed. (H K Versteeg and W Malalasekera) 내용을 참고하였습니다. 본문의 내용은 필자가 공부중인 내용으로 실제와 다르거나 틀린내용일 수 있습니다. |
앞으로 나아가야할 길이 멀지만...
서두르지 않고 CFD에서 가장 기본이 되는 문제에 대해서 다루면서 차근차근 진도를 나가보려고 한다.
따라서 이번 포스팅에서는 '유동이 없을 때 1D-steady state에서의 열전도 문제'를 다뤄보겠다. 1D 문제는 얼마든 2D, 3D로 확장될 수 있다.
① 유동이 없기 때문에 momentum equation, continuity equation은 다루지 않으며 energy equation만 다룬다.
② 1-D steady state 문제로 시간변화항 및 대류항은 무시하며, 확산항 및 소스항만 계산한다.
따라서 아래와 같은 식을 얻을 수 있으며, (eq. 1)

앞 포스팅에서도 유도했듯 검사체적에 대해 적분할 시 eq. 2를 얻을 수 있다.
(실제로 유한체적법에 사용하는 식은 적분식)

전산유체역학의 해를 구하는 과정을 간단하게 설명하자면,
i) 절점으로 나누어진 검사체적(C.V)을
ii) 이산화되어진 지배방정식을 통하여
iii) 얻어진 TDMA를 적절한 행렬 해석기법을 이용하여 푼다.
정확한 검사체적에 대한 명확한 수치를 얻기위한 방법으로 반드시 미분형태의 govern equation을 적분형태로 바꾸는 과정이 필요하다.
Step 1. Grid generation

먼저 문제를 간단화 시킨 Fig. 1을 보면 P라는 control volume과 각각 좌우측에 인접해 있는 W, E라는 Control volume이 존재한다. 그리고 양 끝 노드인 A, B에는 Boundary condition이 지정되어있는 간단한 문제를 그림으로 표현하였다.
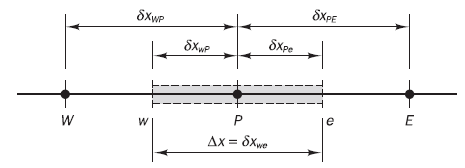
P라는 노드 그리고 그 주변노드와의 dimensional geometry를 구체화 시킨 Fig. 2의 경우에는 Discretisation에 사용할 변수들이 명시되어있다. 각 노드간의 거리는 δXab 형식으로 표현되며 이는 질점 a와 b사이의 거리를 나타낸다. P라는 노드의 양끝의 boundary는 w와 e로 나타내어지므로 노드의 너비(width)는 Δx = δXwe로 나타내어질 수 있다. 옆 노드(W 또는 E)의 중심까지의 거리는 δXwp 및 δXpe로 나타내어진다.
Step 2. Discretisation
다음단계는 이산화이다. 컴퓨터는 단순히 덧셈, 곱셈등의 간단한 사칙연산밖에 하지 못하기 때문에 편미분방정식의 오리지널 형태를 그대로 줄 경우 스스로 해결하지 못한다. 컴퓨터가 해결할 수 있게끔 식을 바꾸어 주는 과정을 이산화(Discretisation)라고 한다. 먼저, 식을 div와 grad를 정의대로 풀어주고 식 전체를 적분형태로 바꾸어 준다. (eq. 3)

bar표시를 한 S는 소스S를 검사체적에 대해 평균한 값을 의미한다.
전산유체역학에서 사용하는 식은 Control volume 측면(물리학적 측면)에서 바라볼 시 매우 직관적으로 해석할 수 있다.
Eq. 3 에서는 diffusion에 의해 west방향에서 유입된 φ에 east방향으로 유출된 φ를 뺀것이(diffusion term) 총 source로 부터의 generation(source term)과 동일하다는, φ의 평형방정식을 보여주고있다.
이러한 평형 방정식을 컴퓨터가 계산해낼 수 있게, 가장 명료하고 대표적인 이산화방법인 centeral differecing을 적용하여 식을 이산화 할 것이다. 이산화 해야 할 변수와 그 방법을 살펴보자면 아래와 같다.
1) 확산 계수 (Γ) - eq. 4
2) 확산 플럭스항 (φ) - eq. 5
3) 소스텀 (S) - eq. 6


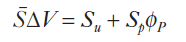
소스텀의 경우에 종속변수의 함수가 될 수 있게끔 유한체적법에서는 eq. 6과 같이 선형적으로 정의한다.
상기한 식(eq. 4~6)을 모두 대입한 이후 eq. 3에 대입하면 아래의 식 eq. 7을 얻을 수 있으며, 이를 다시 정렬하면 더 간결한 최종형태를 얻을 수 있다. (eq. 8) (왜 이와같이 정리하는가?에 대해서는 후술)


해당 식을 eq. 9와 같은 형식으로 정리하여, 변수별로 정리하면 최종형태를 얻을 수 있다. (fig. 3)
최종형태


이로서, 현노드 φp의 좌(φw)/우(φe)와의 관계를 식으로 나타낼 수 있게 되었다. (계수 ap, aw, ae를 이용해서)
계수는 여러가지 정보(area of node, 대류질랑플럭스, 확산 전도도, 경계면온도(경계node의 경우))등을 통하여 어렵지 않게 얻어질 수 있으므로 걱정하지말자.
Step 3. Solution of equation
이와 같은 과정을 모든 절점에서 진행할 시 이산화 방정식이 수립될 것 이며, 한쪽면이 경계인경우 Boundary condition을 반영한 이산화 방정식이 수립될 것 이다. 이러한 방정식이 node 개수만큼 얻어지고 인접한 node간의 상관관계로 나타내어 질 것이므로 TDMA(Tri-diagonal matrix algorithm)으로 해석될 수 있다.

해당식(Eq. 9)의 존재의의를 유체역학적 또는 물리적이 아니라 수학적으로 살펴보자면,
(물리학적으로 살펴 보기 위한 마지노선은 Eq. 7이며 Eq. 9는 수학적인 해결을 위하여 변형한 것 이다.)
결국, φ라는 미지의 값(unknown, node별로 각자의 값을 가지며 전산유체역학으로 계산하기위한 최종 결과물)과
a라는 주어진계수(known, 확산계수 또는 node간의 거리등 알 수 있는 값으로 나타내어진다)로 이루어진 방정식이며,
계수는 area of node, 대류질랑플럭스, 확산 전도도, 경계면온도등을 통하여 얻어진다. (즉, 이미 알려진 값 이다!)
1) 이러한 방정식이 node의 개수만큼 얻어 질 것이며, 2) 이는 인접한 node간의 상관관계로 나타내어진 식이므로
결국 TDMA(Tri-diagonal matrix algorithm)으로 형태로 나타나게 되어, 적절한 행렬 해석기법으로 필히 계산될 수 있다.
즉, 확산만있건 대류만있건 확산과 대류가 함께 있건 또 다른경우건, 각자의 경우마다 특정한 다른 이산화형태가 존재하며 이러한 형태와 주어진 계수들만 알면 TDMA 방법으로 해석될 수 있다.