CFD 기초 : 1-D Diffusion + convection problem (3) - 상류차분법

본 글 내용은 An Introduction to Computational Fluid Dynamics 2ed. (H K Versteeg and W Malalasekera) 내용을 참고하였습니다. 본문의 내용은 필자가 공부중인 내용으로 실제와 다르거나 틀린내용일 수 있습니다.

 

 

앞서 유도한 최종적으로 유도된 대류-확산 방정식 (Eq. 1) 및 연속방정식 (Eq. 2)을 다시한번 살펴보자.

Eq. 1

Eq. 2

 

 

(상세내용은 이전 포스팅 참조)

https://cfd-hihi-123.tistory.com/18

CFD 응용 : 1-D Diffusion + convection problem (1) - 수식유도 / 이산화기법 고찰

 

이번엔 상류차분법을 이용하여 차분을 진행하고 장단점에 대하여 비교해보고자 한다.

 

---

상류차분법 (Upwind differencing scheme)

 

상류차분법은 유동방향에 대한 인지를 바탕으로 유동방향을 고려하여 강한 대류유동에서 중심차분법에 비해 강점이 있는 이산화 기법이다. 따라서 +방향 유동 또는 -방향 유동으로 각각 가정하여 식을 전개할 수 있다. (Fig. 1)

Fig .1

+방향 유동을 가지는경우(eq. 3와 같은 경우), 상류차분법에서는 eq. 4과 같이 가정한다. 가정한 방정식을 중앙차분에서 그랬던것과 같이 eq. 1에 대입하게 되면 eq. 5와 같은 방정식을 얻을 수 있다.

 

 

Eq. 3 Assumption (positive direction flow)

Eq. 4

Eq. 5

 

계수 aw, ae, ap를 알기 위하여 Eq. 6과 같이 정리할 수 있으며, ap = aw + ae의 형태로 나타내기 위하여 Eq. 7과 같이 좌변의 계수에 Fw를 빼고 더한다. (즉, 중심노드의 계수 ap는 Eq. 8과 같이 정리될 수 있다.)

 

Eq. 6

Eq. 7

Eq. 8

 

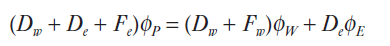
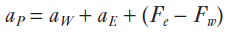
반대로, -방향 유동을 가지는경우(eq. 9와 같은 경우), eq. 10과 같은 가정으로 최종적으로 eq. 11과 같은 방정식을 얻을 수 있다. 마찬가지로 중심노드의 계수 ap는 eq.8과 같이 정리될 수 있다. (단, 한쪽면이 boundary와 맞닿은 양 끝 노드는 우항에 -Sp라는 소스텀을 가진다.)

 

Eq. 9

Eq. 10

 

Eq. 11

 

 

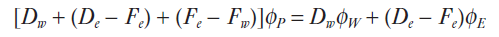
유동이 +방향을 가지는 경우와 -방향을 가지는 경우를 분리하여 정리하면 Fig. 2 조금 더 간단하게 Fig. 3과 같이 정리할 수 있다.

 

Fig. 2

Fig. 3

 

---

상류차분법의 평가

 

1 ) 보존성

 

격자면을 통과하는 플럭스 계산을 위해 일괄성이 있는 표현법을 사용하였으므로, 보존성이 있다.

 

2 ) 유계성

 

모든 계수들은 앞서 진행한 중심차분법과는 다르게 어떠한 경우에도 양수이다 따라서 안정성 있는 해를 얻을 수 있다.

 

3 ) 수송성

 

중심차분법과는 다르게 유동의 방향을 고려하므로 수송성이 식에 포함되어있다고 말할 수 있다.

 

4 ) 정확도

 

backward differencing에 기반한 차분법으로 테일러급수로 나타내었을 때 1차 정확도를 가진다.

또한 보존성, 유계성, 수송성을 모두 만족한다.

 

단, 유동이 격자 선과 정렬되어 있지 않을때 즉, 유동이 직교 격자계에 경사각을 가질 때 수송된 물리량 분포가 확산되게 만드는 거짓확산이라는 특성을 보여준다. 거짓확산은 물리적으로 부정확한 결과를 초래할 수 있으며, 이를 극복하기 위한 방법으로는 격자가 더 fine하게 만드는 것이지만 계산비용이 매우 증가한다. 따라서 엄밀하고 정확한 유동해석을 위해서 상류차분법은 적합하지 않을 수 있다.