CFD 기초 : 1-D Diffusion + convection problem (5) - QUICK 차분법
| 본 글 내용은 An Introduction to Computational Fluid Dynamics 2ed. (H K Versteeg and W Malalasekera) 내용을 참고하였습니다. 본문의 내용은 필자가 공부중인 내용으로 실제와 다르거나 틀린내용일 수 있습니다. |
앞서 유도한 최종적으로 유도된 대류-확산 방정식 (Eq. 1) 및 연속방정식 (Eq. 2)을 다시한번Eq. 6 살펴보자.


(상세내용은 이전 포스팅 참조)
https://cfd-hihi-123.tistory.com/18
CFD 응용 : 1-D Diffusion + convection problem (1) - 수식유도 / 이산화기법 고찰
유체유동이 없는 경우 확산(diffusion)만 고려해도 되지만 대부분의 유체는 유동이 있으므로 대류(convection)의 영향까지 고려해야만 한다. 상단에 있는 적분형의 Transport equation (Eq. 1)을 다시한번 복
cfd-hihi-123.tistory.com
본 포스팅에서는 앞서 사용했던 차분법의 단점을 극복할 수 있는 흔하게 사용되는 고차차분법인 QUICK 차분법을 사용해보자. 상류차분법은 매우 안정적이고 수송성을 만족시키나, 1차 정확도로 오차가 쉽게 발생한다. 중심차분법은 2차 정확도를 가지나 불안정하며 수송성 조건을 위배한다.
따라서 안정성있고 유동방향을 포함하여 수송성을 만족시키는 고차차분법의 도입이 필요하다. QUICK 차분법은 이러한 조건을 만족 시킬 수 있는 전통성있는 고차차분법이다.
이전 차분법 복습
차분법에서의 최종 목표라고 한다면, 지배 방정식에서 노드P에서 이웃한 노드(E, W)와의 경계면 φe 또는 φw를 어떻게 표현하는 것이 효율적인가를 알고싶어하는 것이며, 그 이후에 식을 정리한다던가 하는 나머지 과정은 전부 부수적인 과정 일 뿐이다.

「Eq. 1 에 좌항에 있는 φe와 φw를 어떻게 표현하는가」
가령 중앙차분법에서는 φe와 φw를 아래와 같이 표현하며 (Eq. 3)
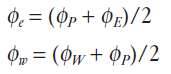
상류차분법은 유동에 방향에 따라 다르지만 유동의 방향이 +인 경우 (Eq. 4)

하이브리드 차분법의 경우 |Pe| < 2 인 경우와 아닌경우로 나누어서 중심차분법 / 상류차분법을 나누어서 적용하며,
멱차분법(power-law scheme)은 Peclet수 10을 기점으로 두 차분법을 나누어 적용한다.
QUICK 차분법 (QUICK differencing)

QUICK 차분법에서는 Eq. 5와 같은 formula를 참조하여 차분법을 사용할 예정이며 i-1 및 i-2로 갈 수록 상류노드(upstream node)이다. QUICK 차분법의 경우에도 수송성을 고려하기 위하여 유동의 방향을 고려한다는 것을 인지해야 한다.

Fig. 1에서 빨간색 타원은 각각 Node WW, W, P, E, EE에서 대류에 의해서 야기되는 유동이며 (Uw, Ue > 0),
w에 우세한 영향을 받는 3개의 node 를 고르자면 Node WW, W, P 3가지 임을 확인할 수 있다.
따라서 절점 w에 대한 식은 Eq. 6과 같이 유도될 수 있으며 e에 대한식은 같은 방법으로 Eq. 7과 같이 유도된다.


여태껏 그래왔던것 처럼 Eq. 1에 대입하면 아래와 같이 정리된다.


그리고 유동 방향이 우측일경우 최종형태는 아래와 같다.


물론 이와다르게 유동의 방향이 반대인 경우도 있겠지만, 매우 유사한 과정을 진행하기 때문에 따로 유도하지는 않을 예정이다. 유동방향을 양쪽 모두 고려한 최종 형태는 아래참조 (Fig. 3 / Eq. 11)


QUICK 차분법의 평가
QUICK 차분법은 일관성있게 격자 면의 플럭스를 계산하므로 보존성이 있고 두개의 상류값과 하나의 하류값에 기초하므로 수송성 또한 가지고 있다. 유계성이 연속성을 만족시킬경우, 계수 ap는 모든 이웃계수들의 합과 동일하며 이는 유계성을 위해 바람직하다. 2차 함수에 기초하여 테일러급수 전개를 하게 된다면 무려 3차 정확도를 가진다.
단점으로는, 주요 계수인 E와 W가 양수임을 보장할 수 없고 계수 a_WW및 a_EE는 음수이다. uw, ue>0인 경우 그리 크지 않는 cell Peclet number (>8/3)에서 동쪽 계수가 음수가 되기 때문에 unbounded 해가 얻어진다. (100~200℃문제에서 범위외의 해가 얻어지는 현상) Peclet number가 높은경우 거짓 진동(위글)을 발생시킨다. 즉, 조건에 따라 안정성이 결정된다.